1로 만들기

코드

n = int(input())
d = [0]*(n+1)
for i in range(2, n+1):
    d[i] = d[i-1] + 1
    if i % 2 == 0:
        d[i] = min(d[i], d[i//2] + 1)
    if i % 3 == 0:
        d[i] = min(d[i], d[i//3] + 1)
print(d[n])

푸는 방법

단순하게 생각해서 반복문과 if문을 사용하여 처음에는 틀렸었다…

예시)

if i%3 ==0:

elif i%2 ==0:

else:
    i -= 1

10의 경우

10 -> 5 -> 4 -> 2 -> 1 이라는 횟수보다
10 -> 9 -> 3 -> 1 이라는 나누기보다 먼저 1을 빼서 구하는 더 짧은 방법이 있기 때문이다.

따라서 이 문제는 다이나믹 프로그래밍이라는 방법으로 풀어주어야한다.

다이나믹 프로그래밍에는

1. 재귀함수를 이용하는 탑다운 방식
2. 단순히 반복문을 이용하는 보텀업 방식

이 있는데 탑다운 방식 보다는 반복문을 사용하는 것이 오버헤드를 줄일 수 있으므로 반복문을 사용한 프로그램이 더 성능이 좋다고 한다.

프로그램을 짜기에 앞서 도식화를 먼저 시켜보면 이해하기가 쉽다.

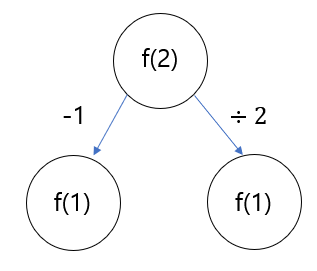
2단계의 경우

---

위 그림에서 f(1)은 구하고자 하는 1을 의미한다.
즉, 그림의 의미는 2에서 1이 된 방법을 의미한다. 문제의 -1을 하는 방법과 나누기 2를 하는 방법 두 가지가 있다.

3단계의 경우

---

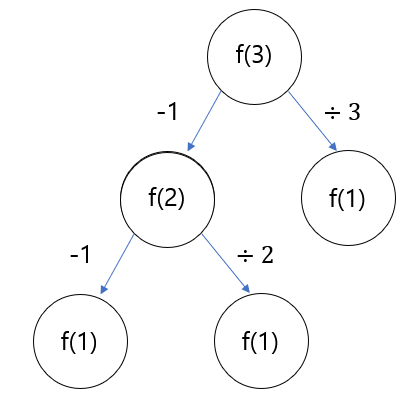
위 그림은 3에서 1이 되는 방법이다.
3에서 1이 되는 방법을 2를 거쳐서 1이 되는 방법
나누기 3을 해서 1이 되는 방법이 있다.

따라서 이 그림을 통해서 알 수 있는 것은 -1을 하는 것 보다 나누기 3을을 해주는 것이 >더 적은 횟수를 통해서 1이 될 수 있다는 것을 확인할 수 있다.

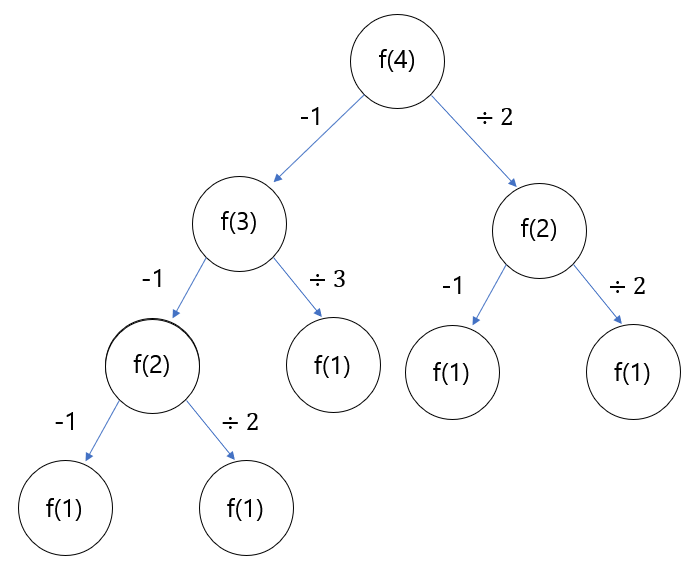
4단계의 경우

---

4는 위 그림과 같다.

이를 프로그램으로 나타내기 위해서는 우선 리스트로 각 단계에서의 최소 횟수를 나타내는 배열을 초기화 해준다(메모이제이션(memoization)).
d = [0] * (n+1) (n이 아닌 n+1인 이유는 리스트의 각 숫자를 n과 맞춰주기 위해서이다. 예를 들어, d[1]은 위 그림에서의 f(1)이다.)

주의할 점은 보텀업 방식이기 때문에 1에서부터 n까지 올라가면서 숫자를 구한다는 것이다.
따라서 상위 숫자는 이미 구해진(메모이제이션(memoization)) 것을 참조해 빠르게 횟수를 구할 수 있다.

다음은 반복문을 통해서 하위 부터 상위로 올라가는 것을 구현한다.

for문으로 2부터 n+1까지 반복한다(1은 횟수가 0이기 떄문에 제외).
이 때 구하는 방법은 먼저 -1을 한 것을 구하고, n/2와 n/3이 되는 경우를 if문으로 찾아서 어느 것이 더 작은지 비교한다.

코드로 구현하면

• 첫번째로 1을 뺴는 경우
  d[i] = d[i-1] + 1로 나타낼 수 있다.(+1을 하는 이유는 위로 올라가면서 횟수를 1씩 증가시키기 위함이다. 따지자면 위 그림에서 화살표를 나타낸다.)
• 두번째로 2로 나누는 경우
  d[i//2] + 1 (//은 소수점 아래는 버리고 정수로 나타내준다.)
• 세번쨰로 3으로 나누는 경우
  d[i//3] + 1

로 나타내는데 주의할 점은 -1로 뺸 경우와 나머지 2와 3으로 나는 경우의 횟수 중에서 누가 더 작은지 비교를 해야한다.

따라서 파이썬의 min() 함수를 이용해주었다.

for i in range(2, 11):
    d[i] = d[i - 1] + 1 #1을 뺸 경우를 나타낸다.
    if i % 2 == 0: #2로 나눌 수 있는 수 인 경우
        d[i] = min(d[i], d[i//2] + 1) #위의 -1와 나누기 2 중 누가 더 작은지 비교
    if i % 3 == 0:
        d[i] = min(d[i], d[i//3] + 1) #위의 -1와 나누기 3 중 누가 더 작은지 비교    
        #혹은 위의 나누기 2와 나누기 3 중 누가 더 적은지 비교(매우 중요함!!)

가장 중요한 점은 i가 2로도 나눠지고 3으로도 나눠지는 경우가 있기 때문에 2로 나눈 if문을 만족하고 조건문 밖으로 나가는 elif가 아닌 if문을 적어 나누기 3과 나누기 2를 비교하고 넘어가야한다는 점이다.

따라서 각 d[i]에는 단계별 가장 적은 횟수가 기록되어 답을 정확하게 구할 수 있다.