카드 구매하기

코드

n = int(input())

p = list(map(int, input().split()))

d = [0] * (n+1)

d[0] = p[0]
for i in range(1, n):
    for j in range(i+1):
        if j == i:
            d[i] = max(d[i], p[i])
        d[i] = max(d[i], d[i-1-j] + p[j])
print(d[n-1])

푸는 방법

핵심 아이디어는 1463번 문제의 1로 만들기와 같다.

작은 단위부터 나눠서 생각하자.

우선 P2가 되는 방법 즉 2장을 갖는 방법은
1 + 1, 2 과 같이 1장이 든 카드팩 2개, 2장이 든 카드팩 1개 이렇게 생각해 볼 수 있다.
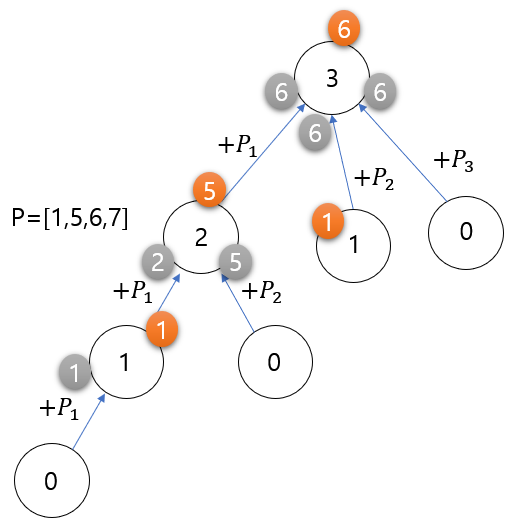
p = [1,5,6,7]로 두자

그림으로 보면 다음과 같다.

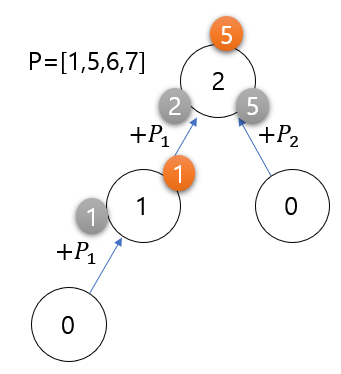
(회색 동그라마는 각 단계를 통해서 합산된 카드팩 금액, 주황색 동그라미는 각 단계를 통해서 >들어온 금액 중 가장 큰 값)

P3을 한 번 더 시행하면

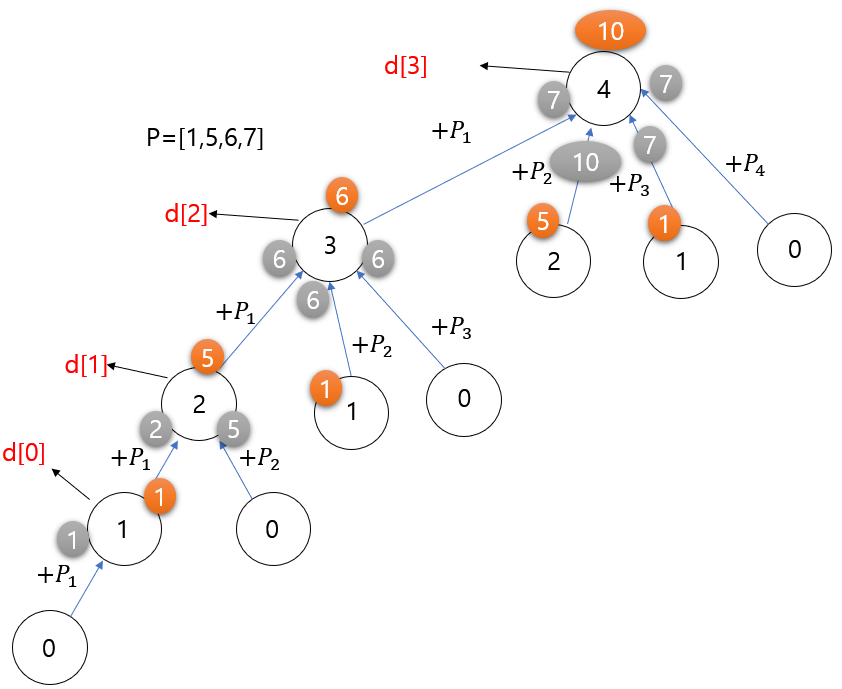
마지막으로 p4를 한 번 더 시행하면

위 와 같은 그림이 된다.

이 때 주황색으로 표기된 동그라미는 메모이제이션을 통해서 기록해 해당 경우가 나올 때마다 반복적으로 사용할 수 있게 만들어 주어야한다.

따라서 d = [0] * (n+1) 로 리스트를 만들어 준다.

처음에 1장이 든 카드팩을 구매하는 방법은 1가지 밖에 없다.
따라서 d[0] = p[0]으로 둘 수 있다.

2장이 든 카드팩을 구하는 방법은 d[1]이 되고 d[0]에서 p[0]을 더해 준 값과 p[1]을 비교해서 더 큰 값으로 갱신해주어야한다. 식으로 나타내면
P2일 경우는 d[1] = max(d[0]+p[0], p[1])
P3일 경우는 d[2] = max(d[1]+p[0], d[0]+p[1], p[2])
P4일 경우는 d[3] = max(d[2]+p[0], d[1]+p[1], d[0]+p[2], p[3]) 과 같이 나타난다.

이를 반복문으로 구현하면

for i in range(n):
    for j in range(i+1):    #예를들어 d[1]일 때는 p[1]까지만 출력되게 하기 위해 범위를 0~i+1까지 설정해야한다.
        if j == i:
            d[i] = max(d[i], p[j]) #가장 마지막은 d[i-1-j] + p[j] 구조가 아니므로 별도로 설정
        d[i] = max(d[i], d[i-1-j] + p[j])

가장 마지막은 p[j]만 나오므로 d[i-1-j] + p[j] 구조가 아니기 때문에 별도로 설정해야하는 것에 주의한다.